Multiplication of 2 two-digit numbers
Multiplication of 2 two-digit numbers where the first digit
of both the numbers are same and the last digit of the two numbers sum to 10
Multiplication of two numbers that differ by 2
(This trick
only works if you have memorized or can quickly calculate the squares of
numbers.
Multiplication of two numbers that differ by 4
(This trick
only works if you have memorized or can quickly calculate the squares of
numbers.
Multiplication of two numbers that differ by 6
(This trick
only works if you have memorized or can quickly calculate the squares of
numbers.
Activity : Sum of all angles of quadrilateral is 360
·
Draw
a Quadrilateral ABCD on colour chart Sheet .
· Cut such four Quadrilaterals on four different sheets.
· Mark ÐA as Ð1 , ÐB as Ð2 , ÐC as Ð3 and ÐD as Ð4 on each quadrilateral as shown in fig .
· Arrange all four angles of quadrilateral one from each colour at one point.
· What you observe ?
· It forms a complete angle i.e 3600
· This shows that sum of all angles of quadrilateral is 3600
· Cut such four Quadrilaterals on four different sheets.
· Mark ÐA as Ð1 , ÐB as Ð2 , ÐC as Ð3 and ÐD as Ð4 on each quadrilateral as shown in fig .
· Arrange all four angles of quadrilateral one from each colour at one point.
· What you observe ?
· It forms a complete angle i.e 3600
· This shows that sum of all angles of quadrilateral is 3600
Squaring by shortcut
Squaring
Let us
take advantage of algebraic identity.
A2 = (A - d)(A + d) + d2
Naturally,
this formula works for any value of d, but we should choose d to be the distance to a number close to A that is easy to multiply.
Examples.
To square the number 23, we let d = 3 to get
232 = 20 x 26 + 32 = 520 + 9 = 529:
To square
48, let d = 2 to get
482 = 50 x 46 + 22 = 2300 + 4 = 2304:
Examples.
2232 = 200 x 246 + 232= 49;200 + 529 = 49;729
9522 = 1000 x 904 + 482 = 904;000 + 2;304 = 906;304:
To do
mental calculations of this size, one needs to be quick at multiplying 2-digit
and 3-digit numbers by 1-digit numbers, generating the answer from left to
right.
Tangram
The tangram
is a dissection puzzle consisting of seven flat shapes, called tans, which
are put together to form shapes. The objective of the puzzle is to form a
specific shape (given only an outline or silhouette) using all seven pieces,
which may not overlap. It was originally invented in China at some unknown
point in history, and then carried over to Europe by trading ships in the early
19th century. It became very popular in Europe for a time then, and then again
during World War I. It is one of the most popular dissection puzzles in the
world.[
Over 6500 different tangram problems have been
compiled from 19th century texts alone, and the current number is ever-growing.
The number is finite, however. Fu Traing Wang and Chuan-Chin Hsiung proved in
1942 that there are only thirteen convex tangram configurations (configurations
such that a line segment drawn between any two points on the configuration's
edge always pass through the configuration's interior, i.e., configurations
with no recesses in the outline).


You can get more picture from google.
Multiplication of two numbers that differ by 2
Multiplication of two numbers that differ by 2
Note :This trick only works if you know the squares of
numbers.
When two numbers differ by 2,
their product is always the square of the number in between these numbers minus
1.
12 x 14 = (13 x 13) - 1 = 169 - 1 = 168
18 x 20 = (19 x 19) - 1 = 361 - 1 = 360
25 x 27 = (26 x26) - 1 = 676 - 1 = 675
13 x 15 = (14 x 14) - 1 = 196 - 1 = 195
13 x 15 = (14 x 14) - 1 = 196 - 1 = 195
15 x 17 = (16 x 16) - 1 = 256 - 1 = 255
16 x 18 = (17 x 17) - 1 = 289 - 1 = 288
Ekādhikena Pūrvena,
Ekādhikena Pūrvena, ("By one more than the previous one") This sūtra means that the prescribed arithmetical operation is either multiplication or division. Both are implied since we may proceed leftward and multiply (and carry-over the excess value to the next leftward column) or we may go rightward and divide (while prefixing the remainder). When dividing by a nine's family denominator, the digit to the left of the nine (previous) is increased by one to obtain the multiplier.
.Examples:
(Proof) This is a simple application of
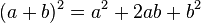 when
when  and
and  , i.e.
, i.e.
It can also be applied in multiplications when the last digit is not 5 but the sum of the last digits is the base (10) and the previous parts are the same. Examples:
 twice combined with the previous result to produce:
twice combined with the previous result to produce:
We illustrate this sūtra by its application to conversion of fractions into their equivalent decimal form. Consider fraction 1/19. Using this formula, this can be converted into a decimal form in a single step. This can be done by applying the formula for either a multiplication or division operation, thus yielding two methods.
.Examples:
- 35×35 = ((3×3)+3),25 = 12,25 and 125×125 = ((12×12)+12),25 = 156,25
- 35×35 = ((3×4),25 = 12,25 and 125×125 = ((12×13),25 = 156,25
(Proof) This is a simple application of
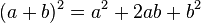 when
when  and
and  , i.e.
, i.e.It can also be applied in multiplications when the last digit is not 5 but the sum of the last digits is the base (10) and the previous parts are the same. Examples:
- 37 × 33 = (3 × 4),7 × 3 = 12,21
- 29 × 21 = (2 × 3),9 × 1 = 6,09 ?
 twice combined with the previous result to produce:
twice combined with the previous result to produce:We illustrate this sūtra by its application to conversion of fractions into their equivalent decimal form. Consider fraction 1/19. Using this formula, this can be converted into a decimal form in a single step. This can be done by applying the formula for either a multiplication or division operation, thus yielding two methods.
Subscribe to:
Comments (Atom)








